In mathematics, an nth root of a number a is a number b such that b=a. When referring to the nth root of a real number a it is assumed that what is desired is the principal nth root of the number, which is denoted radical symbol The principal nth root of a real number a is the unique real number b which is an nth root of a and is of the same sign as a. Note that if n is even, negative numbers will not have a principal nth root. When n = 2, the nth root is called the square root, and when n = 3, the nth root is called the cube root.

Fundamental operations
Often it is simpler to leave the nth roots of numbers "unresolved" (ie. with radicals visible). These unresolved expressions, called "surds", may then be manipulated into simpler forms or arranged to divide each other out. Notationally, the radical symbol (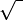) depicts surds, with the upper line above the expression called the vinculum. A cube root takes the form:
, when expressed using indices.
All roots can remain in surd form.
Basic techniques for working with surds arise from identities. Some basic examples include:
The last of these may serve to rationalize the denominator of an expression, moving surds from the denominator to the numerator. It follows from the identity
,
which exemplifies a case of the difference of two squares. Variants for cube and other roots exist, as do more general formulae based on finite geometric series.

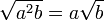
• The above can be combined with index reduction:
  Working with surds
  The radical or root may be represented by the infinite series:
  
  with .
  
  Infinite series
  All the roots of any number, real or complex, may be found with a simple algorithm. The number should first be written in the form ae (see Euler's formula). Then all the nth roots are given by:
  for , where nth root of a.
  
  Finding all roots
  All the complex solutions of x = a, or the nth roots of a, where a is a positive real number, are given by the simplified equation:
  for , where nth root of a.
  
  Solving polynomials
  
  Nth root algorithm
  Shifting nth-root algorithm
  Irrational number
  Algebraic number
  Square root
  Cube root
  Twelfth root of two